Glossary of terms used in theoretical
organic chemistry
[A] [B]
[C] [D] [E]
[F] [G] [H]
[I] [J-K] [L]
[M]
[N] [O] [P]
[Q-R] [S] [T]
[U-V] [W-Z]
J-K
Jahn-Teller (JT) effect -
Deals with molecular distortions due to an electronically degenerate
ground state. For nonlinear
molecular entities in a geometry described by a symmetry
point group possessing degenerate irreducible representations
there always exists at least one nontotally symmetric vibration
that makes the electronic states
with orbital degeneracy unstable at this geometry The nuclei are displaced
to new equilibrium positions of lower symmetry causing a splitting
of the originally degenerate electronic states (first-order Jahn-Teller
effect). In the case of molecules with a nondegenerate ground electron
state, but with a very low lying excited
state, distortions of proper symmetry arise which mix ground
and excited states, and thereby lower the ground
state energy ( pseudo
Jahn-Teller or second-order
Jahn-Teller effect). The closer the states in energy, the
more effective is the mixing. The pseudo Jahn-Teller effect manifests
itself in fluxional behaviour (see
fluxional molecules) and stereochemical
nonrigidity of molecules and ions. BERSUKER
(1984); PEARSON (1983).
See also Vibronic coupling, Peierls
distortion, and Renner effect.
Kinetic stability - The propensity
of a molecular system not to undergo chemical changes in a reasonable
period of time even in the presence of small external perturbations,
owing to a high activation barrier.
Kohn-Sham orbitals - The functions
y(r) in a set of one-electron equations derived
by Kohn and Sham, from which one can obtain the exact electron
density and hence the total
energy.
| Heffyi(r)
= ei
y(r) |
i = 1, 2, ...n |
where Heff is the effective
one-electron hamiltonian, generally expressed as a functional
of electron density, r(r) and
ei are the energies associated
with the yi(r) .
The Kohn-Sham equations are fundamental in density
functional theory as they serve as a starting point for approximate
methods. The electron density r(r)
can be calculated from the yi’s
according to
r(r) =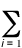 
|yi(r)|2
The Kohn-Sham orbitals yi
should not be confused with the molecular
orbitals obtained in Hartree-Fock
method. They have no physical significance other than in allowing
the exact r(r)
to be calculated by the above equation. KOHN
and SHAM (1965); PARR and YANG (1989);
WEBER, HUBER and WEBER (1993).
Koopmans’ theorem - Directly
relates experimental ionization
potentials with energy levels of molecular
orbitals. The theorem states that the ionization potential required
to remove an electron from the orbital
yi is given by the negative value of the
energy of the orbital, -ei, as calculated
within the Hartree-Fock approximation. The theorem is not applied
to localized molecular orbitals, which are not eigenfunctions
of the effective hamiltonian.
