Glossary of terms used in theoretical
organic chemistry
[A] [B]
[C] [D] [E]
[F] [G] [H]
[I] [J-K] [L]
[M]
[N] [O] [P]
[Q-R] [S] [T]
[U-V] [W-Z]
N
Narcissistic reaction -
The degenerate transformation in which the structure of the products
can be viewed as a reflection of the structure of the reactants
in a mirror plane, which is a symmetry element absent in both the reactants
and the products. An example is the pyramidal inversion of ammonia
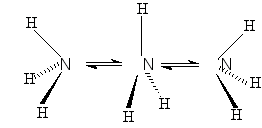
SALEM (1971).
Natural atomic orbital (NAO) -
A valence-shell atomic orbital
whose derivation involves diagonalizing the localized block of the full
density matrix of a given molecule associated with basis
functions ci(A) on that atom.
A distinguishing feature of NAOs is that they meet the simultaneous
requirement of orthonormality and maximum occupancy. For isolated atoms,
NAOs coincide with natural orbitals.
In a polyatomic molecule the NAOs (in contrast to natural orbitals
that become delocalized over all nuclear centers) mostly retain one-center
character, and thus are optimal for describing the molecular
electron density around each
atomic center.
REED, WEINSTOCK, and WEINHOLD (1985).
Natural bond orbital (NBO) - The
orbital which is formed from natural
hybrid orbitals. For a localized s-bond
between atoms A and B, the NBO is :
sAB = cAhA
+ cBhB
where hA and hB are the natural hybrids
centered on atoms A and B. NBOs closely correspond to the picture
of localized bonds and lone pairs as basic units of molecular structure,
so that is possible to conveniently interpret ab initio wavefunctions
in terms of the classical Lewis structure concepts by transforming
these functions to NBO form.
REED, WEINHOLD, and CURTISS (1988).
Natural hybrid orbital (NHO) -
Symmetrically orthogonalized directed hybrid
orbital derived through unitary transformation of natural
atomic orbitals centered on a particular atom.
Natural orbital - The orbitals
defined (P. Löwdin) as the eigenfunctions of the spinless one-particle
electron density matrix. For a configuration
interaction wavefunction
constructed from orbitals f, the electron
density function, r, is of
the form:
r =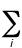 
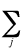aijfi*fj
where the coefficients aij are a set of numbers
which form the density matrix. The NOs reduce the density matrix
r to a diagonal form:
r =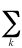 
bkfk*fk
where the coefficients bk are occupation numbers
of each orbital.The importance of natural orbitals is in the fact
that CI expansions based on these orbitals have generally the fastest
convergence. If a CI calculation was carried out in terms of an arbitrary
basis set and the subsequent diagonalization
of the density matrix aij gave the natural orbitals, the same
calculation repeated in terms of the natural orbitals thus obtained
would lead to the wavefunction
for which only those configurations built up from natural orbitals
with large occupation numbers were important. LÖWDIN
(1955); PILAR (1968).
Natural population analysis (NPA)
- The analysis of the electron
density distribution in a molecular system based on the
orthonormal natural atomic orbitals.
Natural populations, ni(A) are the occupancies
of the natural atomic orbitals. These rigorously satisfy the Pauli
exclusion principle:
0 < ni(A) <2. The population of an atom n(A)
is the sum of natural populations
n(A) =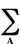 
ni(A).
A distinquished feature of the NPA method is that it largely resolves
the basis set dependence problem encountered in the Mulliken
population analysis method. REED
and SCHLEYER (1990); REED, WEINHOLD,
and CURTISS (1988).
Negative hyperconjugation
- The effect of donation of electron density from filled
p or np-orbitals
to the symmetry adapted s*-orbital(s) of
s-bond(s) of a molecular entity resulting
in building p-character into bonds that nominally
possess only s-character. The consequences
of the effect are, for example, in elongation of the C-F bond in
the b-fluoroethyl anion and stabilization
of the antiperiplanar conformation of fluoromethylamine.
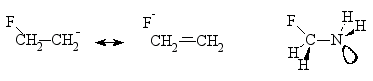
REED and SCHLEYER (1990); SCHLEYER
and KOS (1983).
Nodal plane - A plane of a
system in which the value of the orbital wavefunction equals
zero. This plane defines a region of zero electron
density for the orbital.
Nonadiabatic reaction -
Synonymous with Diabatic
reaction.
Nonbonding molecular orbital
- A molecular orbital
whose occupation by electrons does not contribute (or contributes
insignificantly) to the binding energy
of the molecule. Generally, a nonbonding MO represents the highest
occupied molecular orbital of a molecule
Nonclassical structure
- The structure of molecules or molecular ions that escapes description
in terms of conventional rules of valency and stereochemistry. Nonclassical
structures are characteristic of carbonium ions with hypercoordinated
(see hypercoordination)
carbon atoms, e.g. the ion methanium 1, pyramidal dication
C6H62+, 2 (isomeric to benzene
dication), and the molecular species whose structure cannot be adequately
represented by the equilibrium (2-norbornyl cation, 3) or
resonance of two or more classical structures. From the stereochemical
point of view, those structures are assigned to the nonclassical
type for which all tetracoordinate carbon bonds extend into a single
hemisphere, i.e. the valence angle of a carbon atom is greater than
180o. A hypothetical example is tetracyclo[2.1.0.01,3.02,5]pentane
(pyramidane), 4, the structure of which corresponds to a local
minimum on the C5H4 potential energy surface.
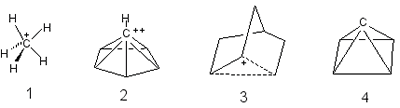
BROWN (1977); MINKIN,
MINYAEV, and ZHDANOV (1987).
Noncrossing rule - Energy levels
of orbitals of the same symmetry cannot cross each other along a reaction
coordinate. The rule is applied also to the energy variation
of electronic states. SALEM
(1982); WOODWARD and HOFFMANN (1969).
Nonempirical quantum mechanical
methods - see Ab initio quantum mechanical
methods.
Non-Kekulé
molecules - Molecules that are fully conjugated, but each of whose
Kekulé structures contains
at least two atoms that are not p-bonded.
Examples of non-Kekulé hydrocarbons are trimethylenemethane
(2-methylidenepropane-1,3-diyl) 1, m-benzoquinodimethane
(benzene-1,3- diyldimethyl) 2, and 1,2,4,5-tetramethylenebenzene
(benzene-1,2,4,5-tetrayltetramethyl) 3.
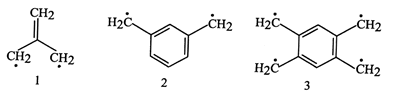
BORDEN, IWAMURA, and BERSON
(1994); LONGUET-HIGGINS (1950).
Normalization - A mathematical procedure
which ensures that the integral of the square of modulus of a wavefunction
over all space equals 1. The constant required to ensure that a wavefunction
is normalized is termed the normalization constant.
