Glossary of terms used in theoretical
organic chemistry
[A] [B]
[C] [D] [E]
[F] [G] [H]
[I] [J-K] [L]
[M]
[N] [O] [P]
[Q-R] [S] [T]
[U-V] [W-Z]
W-Z
Wade's rules - The electron-counting
rules for prediction of stable structures of polyhedral inorganic,
organometallic, and organic compounds. So-called "skeletal" electrons,
i.e. valence electrons of atoms positioned in the vertices of a
molecular polyhedron that form bonding electron pairs of the framework
bonds, are taken into account, their number being determined as follows
Main-group elements k = v + x - 2
Transition metals k = v + x - 12
where v is the full number of valence electrons of an atom or
group in a vertex and x is the number of one-electron ligands.
For deltahedral closo (closed) structures (characterized by triangle
faces) with m vertices there exist (m+1) bonding
molecular orbitals which may be filled with not more than
2m+2 skeletal electrons (m = 4, 5 ...). For nido
(nest-like) structures derived from the closo-forms through
truncation of one apex there are (m+2) bonding MOs which may
be occupied with not more than 2m+4 skeletal electrons. For arachno
(web-like) structures derived from nido-forms through truncation
of one apex, there are (m+3) bonding MOs that may be occupied by
2m+6 electrons.The extension of Wade’s rules is the
polyhedral skeletal electron pair approach that
makes allowance for the total electron count in condensed polyhedra
derived by the condensation of smaller tetrahedral, octahedral,
and trigonal-prismatic fragments. The total electron count in a
condensed polyhedron is equal to the sum of the electron counts for
the parent polyhedra A and B minus the electron count characteristic
of the atom, pair of atoms, or face of atoms common to both polyhedra.
MINGOS (1984); WADE
(1976).
Walsh diagram (also called Walsh-Mulliken
diagram) - A molecular orbital diagram where the orbitals
in one reference geometry are correlated in energy with the orbitals
of the deformed structure.
Walsh's rules - The summaries
of observations that the shapes of molecules in a given structural class
are determined by the number of valence electrons. The most important
rule states that a molecule adopts the structure that best stabilizes
its highest occupied molecular
orbital. If the HOMO is unperturbed by the structural change
under consideration, the occupied MO lying closest to it governs
the geometric preference.
Wavefunction
- A mathematical expression whose form resembles the wave equations
of physics, supposed to contain all the information associated with
a particular atomic or molecular system,. When a wavefunction is
operated on by certain quantum mechanical operators, a theoretical evaluation
of physical and chemical observables for that system (the most important
one being energy) can be carried out.
Wave vector - The vector which appears
in the expression of a crystal orbital
as a result of the application of the periodic boundary conditions
to the wavefunction of a solid. It
determines the symmetry and nodal properties of the crystal orbital.
Given the periodic nature of the Bloch orbitals, all the non-equivalent
wavefunctions are generated by the components of the wave vector with
values within the Brillouin zone.
Wigner rule (also known as spin-conservation
rule) - During an elementary chemical step, electronic
and nuclear magnetic moments conserve their orientation.
Woodward-Hoffmann rules -
Electron-counting rules
allowing predictions of thermally and photochemically driven symmetry
allowed and symmetry
forbidden concerted reactions.
Zero differential overlap (ZDO)
approximation - An approach to the systematic neglect of
the small-in-value electron repulsion integrals which is used in
a number of approximate self- consistent
field molecular orbital schemes. It means that all the products
of atomic orbitals cmcn
are set to zero and the overlap
integral Smn = dmn
(where dmn is the Kronecker delta).
The ZDO approximation greatly simplifies the computation of wavefunctions
by eliminating many of two-electron integrals. At the ZDO approximation
all three- and four-centered integrals vanish.
Zero-order wavefunction
- Commonly, the wavefunction used
as a starting point to include
electron correlation effects. Very often the zero-order wavefunction
is a single determinant SCF wavefunction as in MP2, coupled cluster
and CI methods, but it can be a multideterminant wavefunction as in
the MRCI approach.
Zero-point energy (ZPE) - synonymous with
zero-point vibrational energy.
Zero-point vibrational energy
(ZPVE) - The energy of vibration of a molecule at absolute zero
(0 K). It is given by
Evib(0) = (1/2)h 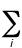 ni
ni
where ni
is a normal-mode vibrational frequency. Even for a small molecule, the
total ZPE can amount to several tens of kcal/mol. ZPE is a quantum
mechanical effect which is a consequence of the uncertainty
principle.

